Introduction
A nice and powerful way to specify 2D fractals like we do in our Android game The Last Dimension are L-Systems or Lindenmayer systems. They can be implemented as a context-free grammar, meaning that there is just a set of substitution rules which get applied when a certain zoom factor is reached. The result therefore provides a more detailed description of the local fractal, which basically resembles the self-similarity a fractal is known for.
This part should give a small introduction to these systems. Now, three components are necessary for simple fractals:
- The axiom
- The angle
- The rules
The turtle
But first to understand how L-Systems draw fractals, you should try to imagine a creature called ‘turtle’ that goes through each symbol step-by-step and executes its meaning. Therefore, first some important symbols in L-Systems:
- letters F, G, H, I, ..: turtle goes forward and draws a line
- +: turtle turns left
- -: turtle turns right
- often small f: turtle goes forward without drawing a line
Thats all commands we need in the beginning!
Axiom and angle
Now we can start with the axiom. The axiom is also a rule, but unique in that way that it does not describe the transformation for zooming but the inital shape of the fractal. But the axiom alone does not specify the final form. As + and – do not specify the angle, we need to give it to the turtle in the beginning. With these two we can draw the first shapes!
axiom: F-F-F-F angle: 90
and that’s a square! Now we can go further and you might guess what this is…
axiom F-F-F angle: 120
Yep, a triangle! Nevertheless, zooming isn’t very spectacular…
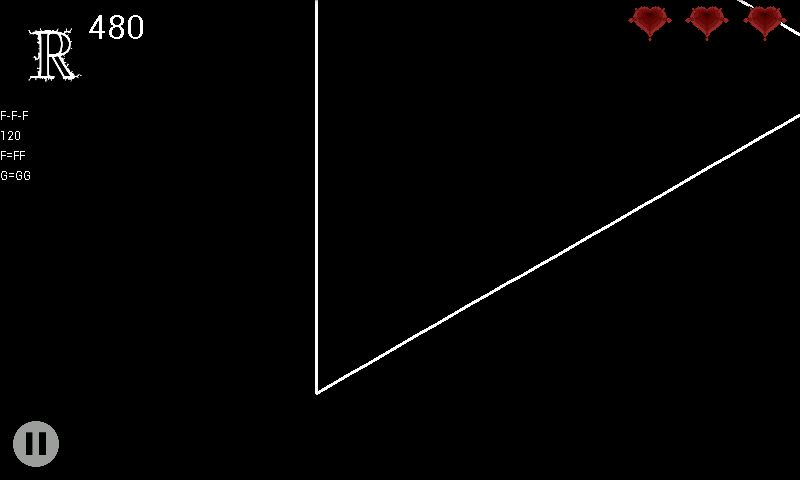
so we need rules!
Rules
Finally! You might already have seen the statements F=FF and G=GG in the screenshots. Those are the simplest rules one could have: If we zoom into the fractal, at one point, the lines will get divided into half, which will obviously look perfectly the same.
But what if we do the following: We could split one line of the triangle in half, but after drawing the first F (red) draw a smaller triangle with -G (orange). Then we jump around with -f-f (yellow&green) and finish with a G (blue). Note that we are limited with the current angle in rotating. So F always draws step 2 (here orange) while the G lines do nothing.
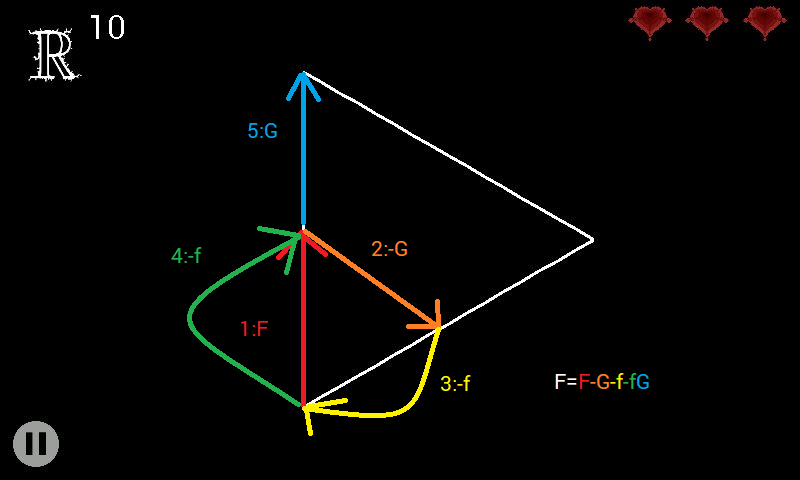Therefore, we also need to adapt the axiom a bit:
axiom: F-G-G rule 1: F-G-f-fG rule 2: G=GG angle: still 120
What does this result in?
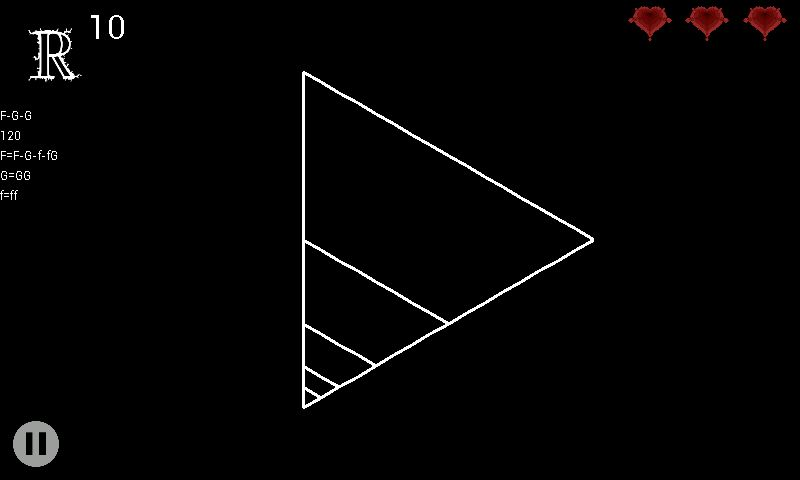
Exactly, we can zoom into the corner and get an endless stream of small triangles!
Changing the axiom to F-F-F puts these fractal corners in every corner:
Now this is basically the process of working with L-Systems! One could now tweak a bit, and with certain extensions to the system, one can create famous basic fractals like the Sierpiński triangle. Try it out yourself at e.g. https://onlinemathtools.com/l-system-generator!
With the color, this now already looks very similar to the first level of The Last Dimension, Natural Logarithm! If you look carefully, you can see an additional command in the axiom. But those extensions are a topic for another post. I hope that I was able to give a nice overview over L-Systems. See you 😉
